NumPy实现多维数组中的线性代数代码示例

本篇文章小编给大家分享一下NumPy实现多维数组中的线性代数代码示例，文章代码介绍的很详细，小编觉得挺不错的，现在分享给大家供大家参考，有需要的小伙伴们可以来看看。

图形加载和说明

熟悉颜色的朋友应该都知道，一个颜色可以用R，G，B来表示，如果更高级一点，那么还有一个A表示透明度。通常我们用一个四个属性的数组来表示。

对于一个二维的图像来说，其分辨率可以看做是一个X*Y的矩阵，矩阵中的每个点的颜色都可以用（R，G，B）来表示。

有了上面的知识，我们就可以对图像的颜色进行分解了。

首先需要加载一个图像，我们使用imageio.imread方法来加载一个本地图像，如下所示：

import imageio
img=imageio.imread('img.png')
print(type(img))

上面的代码从本地读取图片到img对象中，使用type可以查看img的类型，从运行结果，我们可以看到img的类型是一个数组。

class 'imageio.core.util.Array'

通过img.shape可以得到img是一个(80, 170, 4)的三维数组，也就是说这个图像的分辨率是80*170，每个像素是一个（R，B，G，A）的数组。

最后将图像画出来如下所示：

import matplotlib.pyplot as plt
plt.imshow(img)

图形的灰度

对于三维数组来说，我们可以分别得到三种颜色的数组如下所示：

red_array = img_array[:, :, 0]
green_array = img_array[:, :, 1]
blue_array = img_array[:, :, 2]

有了三个颜色之后我们可以使用下面的公式对其进行灰度变换：

Y=0.2126R + 0.7152G + 0.0722B

上图中Y表示的是灰度。

怎么使用矩阵的乘法呢？使用 @ 就可以了：

 img_gray = img_array @ [0.2126, 0.7152, 0.0722]

现在img是一个80 * 170的矩阵。

现在使用cmap="gray"作图：

plt.imshow(img_gray, cmap="gray")

可以得到下面的灰度图像：

灰度图像的压缩

灰度图像是对图像的颜色进行变换，如果要对图像进行压缩该怎么处理呢？

矩阵运算中有一个概念叫做奇异值和特征值。

设A为n阶矩阵，若存在常数λ及n维非零向量x，使得Ax=λx，则称λ是矩阵A的特征值，x是A属于特征值λ的特征向量。

一个矩阵的一组特征向量是一组正交向量。

即特征向量被施以线性变换 A 只会使向量伸长或缩短而其方向不被改变。

特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。

假如A是m * n阶矩阵，q=min(m,n)，A*A的q个非负特征值的算术平方根叫作A的奇异值。

特征值分解可以方便的提取矩阵的特征，但是前提是这个矩阵是一个方阵。如果是非方阵的情况下，就需要用到奇异值分解了。先看下奇异值分解的定义：

A=UΣVT

其中A是目标要分解的m * n的矩阵，U是一个 m * m的方阵，Σ 是一个m * n 的矩阵，其非对角线上的元素都是0。VTV^TVT是V的转置，也是一个n * n的矩阵。

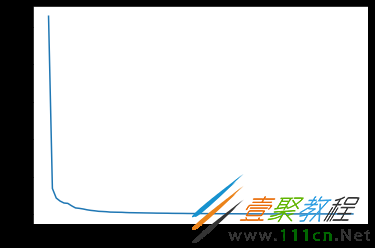
奇异值跟特征值类似，在矩阵Σ中也是从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵。r是一个远小于m、n的数，这样就可以进行压缩矩阵。

通过奇异值分解，我们可以通过更加少量的数据来近似替代原矩阵。

要想使用奇异值分解svd可以直接调用linalg.svd 如下所示：

U, s, Vt = linalg.svd(img_gray)

其中U是一个m * m矩阵，Vt是一个n * n矩阵。

在上述的图像中，U是一个(80, 80)的矩阵，而Vt是一个(170, 170) 的矩阵。而s是一个80的数组，s包含了img中的奇异值。

如果将s用图像来表示，我们可以看到大部分的奇异值都集中在前的部分：

这也就意味着，我们可以取s中前面的部分值来进行图像的重构。

使用s对图像进行重构，需要将s还原成80 * 170 的矩阵：

# 重建
import numpy as np
Sigma = np.zeros((80, 170))
for i in range(80):
    Sigma[i, i] = s[i]

使用 U @ Sigma @ Vt 即可重建原来的矩阵，可以通过计算linalg.norm来比较一下原矩阵和重建的矩阵之间的差异。

linalg.norm(img_gray - U @ Sigma @ Vt)

或者使用np.allclose来比较两个矩阵的不同：

np.allclose(img_gray, U @ Sigma @ Vt)

或者只取s数组的前10个元素，进行重新绘图，比较一下和原图的区别：

k = 10
approx = U @ Sigma[:, :k] @ Vt[:k, :]
plt.imshow(approx, cmap="gray")

可以看到，差异并不是很大：

原始图像的压缩

上一节我们讲到了如何进行灰度图像的压缩，那么如何对原始图像进行压缩呢？

同样可以使用linalg.svd对矩阵进行分解。

但是在使用前需要进行一些处理，因为原始图像的img_array 是一个(80, 170, 3)的矩阵--这里我们将透明度去掉了，只保留了R，B，G三个属性。

在进行转换之前，我们需要把不需要变换的轴放到最前面，也就是说将index=2，换到index=0的位置，然后进行svd操作：

img_array_transposed = np.transpose(img_array, (2, 0, 1))
print(img_array_transposed.shape)

U, s, Vt = linalg.svd(img_array_transposed)
print(U.shape, s.shape, Vt.shape)

同样的，现在s是一个(3, 80)的矩阵，还是少了一维，如果重建图像，需要将其进行填充和处理，最后将重建的图像输出：

Sigma = np.zeros((3, 80, 170))

for j in range(3):
    np.fill_diagonal(Sigma[j, :, :], s[j, :])

reconstructed = U @ Sigma @ Vt
print(reconstructed.shape)

plt.imshow(np.transpose(reconstructed, (1, 2, 0)))

当然，也可以选择前面的K个特征值对图像进行压缩：

approx_img = U @ Sigma[..., :k] @ Vt[..., :k, :]
print(approx_img.shape)
plt.imshow(np.transpose(approx_img, (1, 2, 0)))

重新构建的图像如下：

对比可以发现，虽然损失了部分精度，但是图像还是可以分辨的。