利用Matlab绘制各类特殊图形代码实例

本篇文章小编给大家分享一下利用Matlab绘制各类特殊图形代码实例，文章代码介绍的很详细，小编觉得挺不错的，现在分享给大家供大家参考，有需要的小伙伴们可以来看看。

Matlab绘图介绍

强大的绘图功能是Matlab的特点之一，Matlab提供了一系列的绘图函数，用户不需要过多的考虑绘图的细节，只需要给出一些基本参数就能得到所需图形，这类函数称为高层绘图函数。此外，Matlab还提供了直接对图形句柄进行操作的低层绘图操作。这类操作将图形的每个图形元素（如坐标轴、曲线、文字等）看做一个独立的对象，系统给每个对象分配一个句柄，可以通过句柄对该图形元素进行操作，而不影响其他部分。

Matlab绘制特殊图形

1. 绘制极坐标图

说明：使用polarplot函数绘制极坐标图，每组数据表示一条闭合曲线，共有20条曲线构成20条封闭同心曲线。

t = linspace(0,2*pi,500);
y = 1+0.3*sin(20*t)+0.1*sin(30*t)+0.1*sin(40*t); 
polarplot(t,y,t,1.1*y,t,1.2*y,t,1.3*y,t,1.4*y,t,1.5*y,t,1.6*y,t,1.7*y,t,1.8*y,t,1.9*y,...
    t,2.0*y,t,2.1*y,t,2.2*y,t,2.3*y,t,2.4*y,t,2.5*y,t,2.6*y,t,2.7*y,t,2.8*y,t,2.9*y,'linewidth',1.5);

2. 单条曲线绘制分段函数（反比例函数y=1/x）

说明：反比例函数在x接近于0时，趋近于奇异（1/0 趋近于无穷大），使用nan非数对图形进行镂空，可以实现一条曲线绘制y=1/x的整个定义域。

x = linspace(-3,3,500);
f = @(x) 1./x;
y = f(x);
for ii = 1:length(x)
    if  abs(x(ii))<0.03 
        x(ii) = nan;
        y(ii) = nan;
    end
end
plot(x,y)
legend('y=1/x')

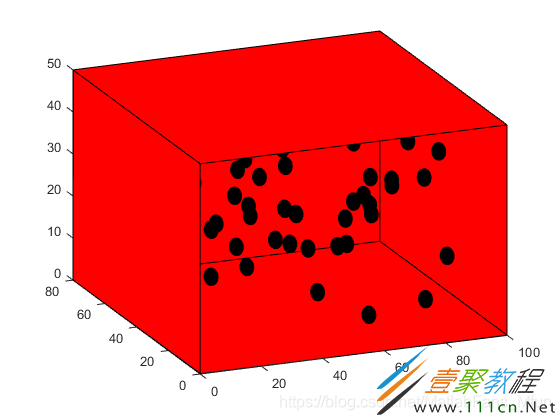
3. 正方体内绘制随机分布的颜色片图

说明： 使用plot3绘制正方体12条边，使用fill3函数绘制颜色片，颜色片位置和填充颜色随机生成。

a = 20;
b = 20;
c = 20;
A1 = [0 0 0
     a 0 0
     a b 0
     0 b 0
     0 0 0];
A2 = [0 0 c
     a 0 c
     a b c
     0 b c
     0 0 c]; 
A3 = [0 0 0
     0 0 c
     0 b c
     0 b 0
     0 0 0]; 
A4 = [a 0 0
     a 0 c
     a b c
     a b 0
     a 0 0];  
% 绘图
figure
hold on
plot3(A1(:,1),A1(:,2),A1(:,3),'k');
plot3(A2(:,1),A2(:,2),A2(:,3),'k');
plot3(A3(:,1),A3(:,2),A3(:,3),'k');
plot3(A4(:,1),A4(:,2),A4(:,3),'k');
view(3)
 
XYZ0 = [0 0 0
        1 0 0
        1 0 1
        0 0 1];
for ii = 1:100
    p = [rand*(a-2) rand*(b-2) rand*(c-2)]+1;    % 球心
    X2=  p(1) + XYZ0(:,1);
    Y2 = p(2) + XYZ0(:,2);
    Z2 = p(3) + XYZ0(:,3);
    ColorSpec = rand(1,3);
    fill3( X2,Y2,Z2,ColorSpec )
end

4. 在大圆内随机生成若干互不相交的小圆

说明：先绘制大圆，在大圆内随机生成小圆圆心，判断小圆圆心和其它小圆的距离，如果小圆圆心距离小于直径，说明小圆相交，舍去该小圆。

tic
X = [];
Y = [];
n = 0;
while n < 1000
    r = rand * (750-5);
    theta = rand * 2*pi;
    x0 = r*cos(theta);
    y0 = r*sin(theta);
    s = min( (x0-X).^2 + (y0-Y).^2 );   % 最小圆心距离
    if s < 10^2
        continue;
    else
        X = [X;x0];   % 圆心坐标集合
        Y = [Y;y0];  
        n = n +1      % 点数
    end
end
toc
alpha = linspace(0,2*pi,100);
x = 5*cos(alpha);
y = 5*sin(alpha);
 
figure
plot( 150*x,150*y,'r' )
hold on
for ii = 1:n
    x0 = X(ii);
    y0 = Y(ii);
    plot(x0+x,y0+y,'k')
end

5. 在长方体内随机生成若干球体

说明：patch函数绘制长方体和球体表面，并可填充颜色。

x = 100;
y = 80;
z = 50;
theta = linspace(0,2*pi,50);
phi = linspace(0,2*pi,50);
[theta,phi] = meshgrid(theta,phi);
r = 2;
X0 = r*cos(phi).*cos(theta);
Y0 = r*cos(phi).*sin(theta);
Z0 = r*sin(phi);

% 绘图
X = [0 x x 0 
     0 x x 0
     0 0 0 0
     x x x x
     0 x x 0]';
Y = [0 0 y y
     0 0 y y
     0 y y 0
     0 y y 0
     y y y y]';
Z = [0 0 0 0
     z z z z
     0 0 z z
     0 0 z z
     0 0 z z ]';
figure
patch(X,Y,Z,'r');
view(3)
hold on
for ii = 1:50
    p = [rand*(100-4*r) rand*(80-4*r) rand*(50-4*r)]+2*r;    % 球心
    X2= p(1) + X0;
    Y2 = p(2) + Y0;
    Z2 = p(3) + Z0;
    patch( X2,Y2,Z2,'y' )
end

6. 绘制圆柱体与球体曲面相交，并绘制相交曲线

说明: mesh函数绘制曲面图，求解方程得到交线参数方程，plot3函数绘制三维交线。

%% 曲面1
t = linspace(0,2*pi,200);
s = linspace(0,2*pi,200);
[t,s] = meshgrid(t,s);
x = 2*cos(t);
y = 2*sin(t).*cos(s);
z = 2*sin(t).*sin(s);
figure
mesh(x,y,z)
%% 曲面2
t2 = linspace(0,2*pi,200);
z2 = linspace(-3,3,200);
[t2,z2] = meshgrid(t2,z2);
x2 = 1 + cos(t2);
y2 = sin(t2);
hold on
mesh(x2,y2,z2)
%% 交线
t3 = linspace(0,2*pi,200);
y3 = sin(t3);
x3 = 1 + cos(t3);
z3 = sqrt(4-2*x3);
plot3(x3,y3,z3,'r','linewidth',5)
hold on
plot3(x3,y3,-z3,'r','linewidth',5)

8. 绘制三维抛物曲面

说明：使用nan非数对图形进行镂空

x = -20:0.1:20;
y = -20:0.1:20;
[X,Y] = meshgrid(x,y);
p = 0.2;
q = 0.1;
Z = X.^2/(2*p) +  Y.^2/(2*q);
Z = (Z<=500) .* Z + ((Z>500)-1) ./ ((Z>500)-1);   % 图形镂空
mesh(X,Y,Z)

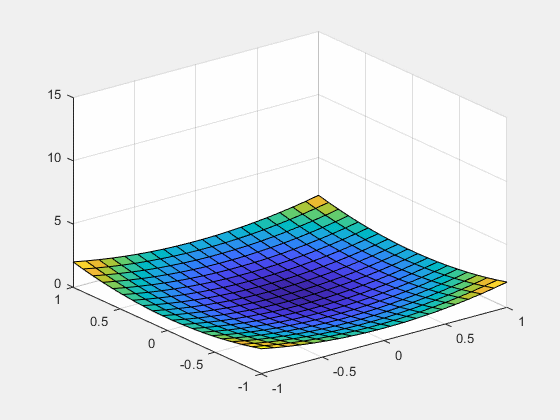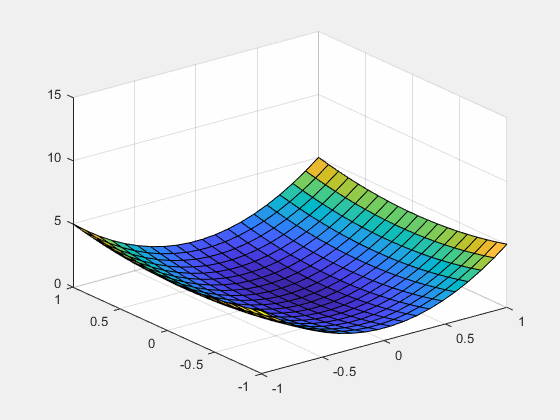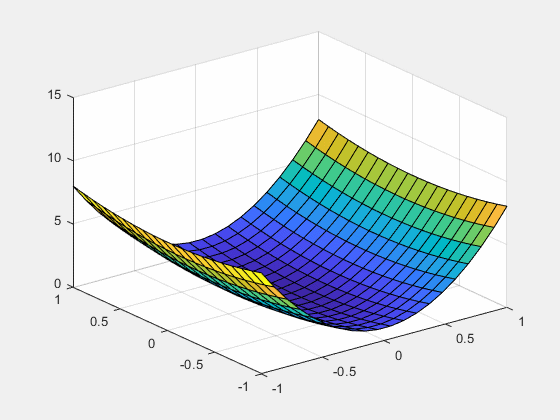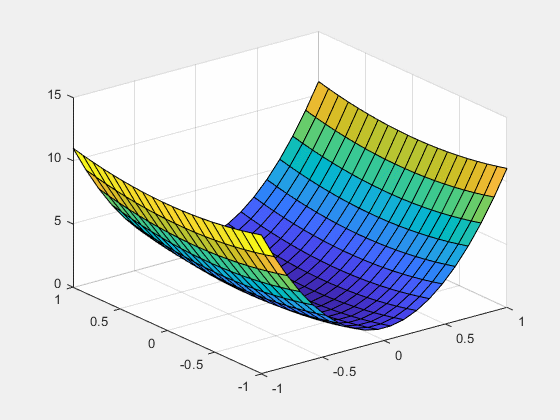
9. 抛物曲面随参数变化形成动画

说明：每个步长内动态更新绘制三维曲面，形成动画效果。

x = linspace(-1,1,20);
y = linspace(-1,1,20);
[X,Y] = meshgrid(x,y);
figure
a = 1;
Z = a.*X.^2 + Y.^2;
h = surf(X,Y,Z);
zlim([0,15])
for a = 1:0.1:10
    Z = a.*X.^2 + Y.^2;
    set(h,'zdata',Z);
    drawnow
    pause(0.1)
end

10. 使用不同频率的正弦波合成方波

说明：傅里叶级数，利用不同频率的正弦波合成方波，三角函数项数越多，合成方波越精确。

t=0:0.000001:1;
 f1=6*sin(10*pi*t)/pi;
 f2=6*sin(10*pi*t)/pi+2*sin(30*pi*t)/pi;
 f3=6*sin(10*pi*t)/pi+2*sin(30*pi*t)/pi+6*sin(50*pi*t)/(5*pi);
 %% 循环段
 N = 10;   % 点数
 f4 = 0;   % 初始值
 for ii = 1:N
     f4 = f4 + 3*2*sin((2*ii-1)*10*pi*t)/pi/(2*ii-1);
 end
 figure
 subplot(2,2,1),plot(t,f1)
 subplot(2,2,2),plot(t,f2) 
 subplot(2,2,3),plot(t,f3)
 subplot(2,2,4),plot(t,f4)