Python排序算法之插入排序及其优化方案代码解析

本篇文章小编给大家分享一下Python排序算法之插入排序及其优化方案代码解析，文章代码介绍的很详细，小编觉得挺不错的，现在分享给大家供大家参考，有需要的小伙伴们可以来看看。

一、插入排序

插入排序与我们平时打扑克牌非常相似，将新摸到的牌插入到已有的牌中合适的位置，而已有的牌往往是有序的。

1.1 执行流程

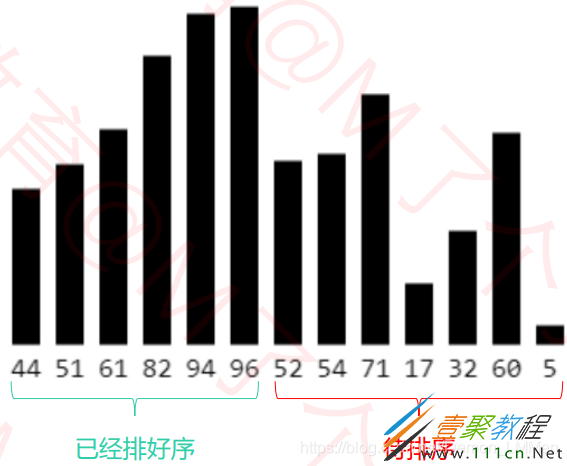
（1）在执行过程中，插入排序会将序列分为2部分，头部是已经排好序的，尾部是待排序的。

（2）从头开始扫描每一个元素，每当扫描到一个元素，就将它插入到头部合适的位置，使得头部数据依然保持有序

1.2 逆序对

数组 <2,3,8,6,1> 的逆序对为：<2,1> ❤️,1> <8,1> <8,6> <6,1>，共5个逆序对。

插入排序的时间复杂度与逆序对的数量成正比关系，逆序对的数量越多，插入排序的消耗的时间就越多。

当逆序对的数量极少时，插入排序的效率特别高，甚至速度比 O nlogn 级别的快速排序还要快。

1.3 代码实现

将一个元素插入到数组有序的前半部分中，那个插入的位置元素一定是比该元素大，而该位置前的元素比该元素小（或者是没有前一个元素）。所以我们可以通过比较，将该元素进行冒泡：如果前一个元素比我大，则交换位置，否则停止冒泡。

def insertion_sort_ver1(array):
    n=len(array)
    for right in range(1,n):
        cur=right
        while cur>0 and array[cur-1]>array[cur]:
            array[cur-1],array[cur]=array[cur],array[cur-1]
            cur-=1

整体代码：

import numpy as np
import time

#检查是否有序
def orderCheck(array):
    for i in range(len(array)-1):
        if array[i]>array[i+1]:
            print('排序失败')
            return
    print('排序成功')
    
def sort(sort_algorithm,ori_array):
    #先复制一份数组，再进行更改
    array = np.copy(ori_array)
    start=time.clock()
    sort_algorithm(array)
    end=time.clock()
    total_time=float(end-start)
    print(sort_algorithm.__name__+" : %0.5f" % total_time)
    orderCheck(array)

def insertion_sort_ver1(array):
    n=len(array)
    for right in range(1,n):
        cur=right
        while cur>0 and array[cur-1]>array[cur]:
            array[cur-1],array[cur]=array[cur],array[cur-1]
            cur-=1
            
array=np.random.randint(0,10000,2000,dtype=int)
sort(insertion_sort_ver1, array)

消耗时间为0.82632秒。

1.4 优化1

在冒泡中，交换前后cur和cur-1位置两个元素的位置，需要进行两次赋值，但如果冒泡仍要继续，cur-1位置的元素还是会被cur-2位置的元素覆盖，所以两次赋值中的一次其实是无意义的，为此我们可以先找到插入位置，然后将后方的元素作统一的移动；或者是在冒泡过程中只进行一次赋值（将前一个元素移动到后方），直到冒泡结束确定插入位置后，再进行待插入元素的插入。

#元素交换作优化
def insertion_sort_ver2(array):
    n=len(array)
    for right in range(1,n):
        cur=right
        elem=array[cur]
        while cur>0 and array[cur-1]>elem:
            array[cur]=array[cur-1]
            cur-=1
        array[cur]=elem

消耗时间为0.45987秒，明显变快了。

1.5 优化2

之前我们在寻找插入的位置时，采用的是从大到小依次遍历的方法，因为是在一个有序的数组上寻找插入的位置，我们肯定会想到一种查找的方法：二分查找。通过二分查找，我们可以通过O(logn)级别的比较与O(n)级别的元素移动完成排序任务，而之前我们进行的比较和移动，都是O(n)级别。

1.5.1 普通二分查找

普通的二分查找十分简单，根据中间位置元素大小更新两端索引位置即可，在此两端的索引 [left,right)采用左闭右开的方式，这样未查找到元素的条件就十分简单，因为区间左闭右开，当left

def binary_search(array,target):#[left,right)左闭右开
    left=0
    right=len(array)
    while left> 1
        if target

	1.5.2 二分查找插入位置


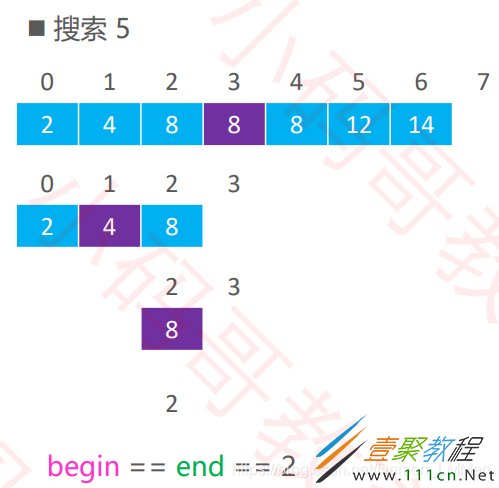
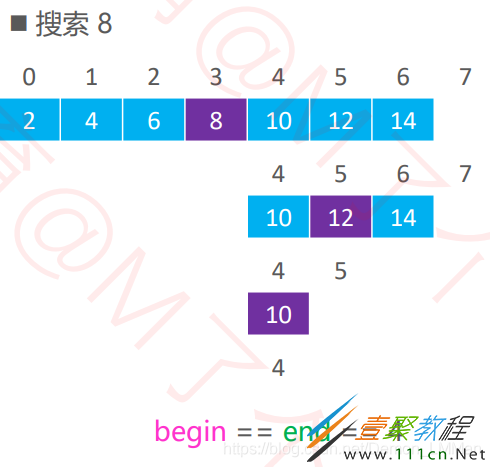
	查找插入位置的二分查找显然和普通二分不同，在此我们修改一下左右端点移动的条件与移动方式。在此左右端点依旧左闭右开，如果当array[middle]小于或等于插入元素target，那么显然middle不可能是插入位置，middle位置的元素也不再需要，left应该为middle+1；而当array[middle]大于target，那么middle有可能是插入的位置（插入位置大于target，前一个元素如果存在，应小于target），应该保留middle，所以right=middle。但是区间是左闭右开，right不可取到，哪怕right=middle，middle不还是无法取得吗？但由于array[middle]不论取何值（不管是大于、等于、小于），都将导致左右端点left、right的变化，且数组中左右端点代表区间的大小是不断减小的，最终左右端点重合，此时的位置就是插入的位置。


	下面是查找的示例：


	


	


	


	


	


	代码如下：

def binary_search(array,index):
    left=0
    right=index
    while left>1
        if array[middle]>array[index]:#大于目标，可能是插入的位置，用right保留
            right=middle
        else:#小于等于，不可能是插入位置，更新left为middle+1
            left=middle+1
    return left #最后插入的位置


	1.5.3 使用二分的插入排序


	找到插入位置后，我们只需移动位置后面的元素，再将元素插入即可。

#利用二分查找找到插入的点，减少了比较的次数
def insertion_sort_ver3(array):
    n=len(array)
    for right in range(1,n):
        index=binary_search(array,right)
        elem=array[right]
        for i in range(right,index,-1):
            array[i]=array[i-1]
        array[index]=elem


	


	可见速度比之前的插入排序仍有提高。


	1.6 时间空间复杂度


	最坏、平均时间复杂度：O(n^2)，最好时间复杂度：O(n)，空间复杂度：O(1)。


	1.7 稳定性


	插入排序将后方的元素从后往前插入，后边相等的元素将插入在左边相等元素的右侧，没有改变原有的位置，属于稳定排序。
                    


                    

                        

                            
相关文章
                        
                        

                                                                                                

                                        人们熟悉的寄居蟹属于以下哪种分类   神奇海洋11月21日答案
                                        11-21
                                    
                                                                    

                                        第五人格11.22共研服有什么更新 11月22日共研服更新内容介绍
                                        11-21
                                    
                                                                    

                                        原神恰斯卡怎么培养
                                        11-21
                                    
                                                                    

                                        无期迷途四星装束是谁
                                        11-21
                                    
                                                                    

                                        王者荣耀帝丹高中校服怎么获得
                                        11-21
                                    
                                                                    

                                        光遇姆明季后续版本怎么玩
                                        11-21