最新下载
热门教程
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
PyTorch检查模型梯度是否可导代码示例
时间:2022-06-25 01:57:40 编辑:袖梨 来源:一聚教程网
本篇文章小编给大家分享一下PyTorch检查模型梯度是否可导代码示例,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
一、PyTorch 检查模型梯度是否可导
当我们构建复杂网络模型或在模型中加入复杂操作时,可能会需要验证该模型或操作是否可导,即模型是否能够优化,在PyTorch框架下,我们可以使用torch.autograd.gradcheck函数来实现这一功能。
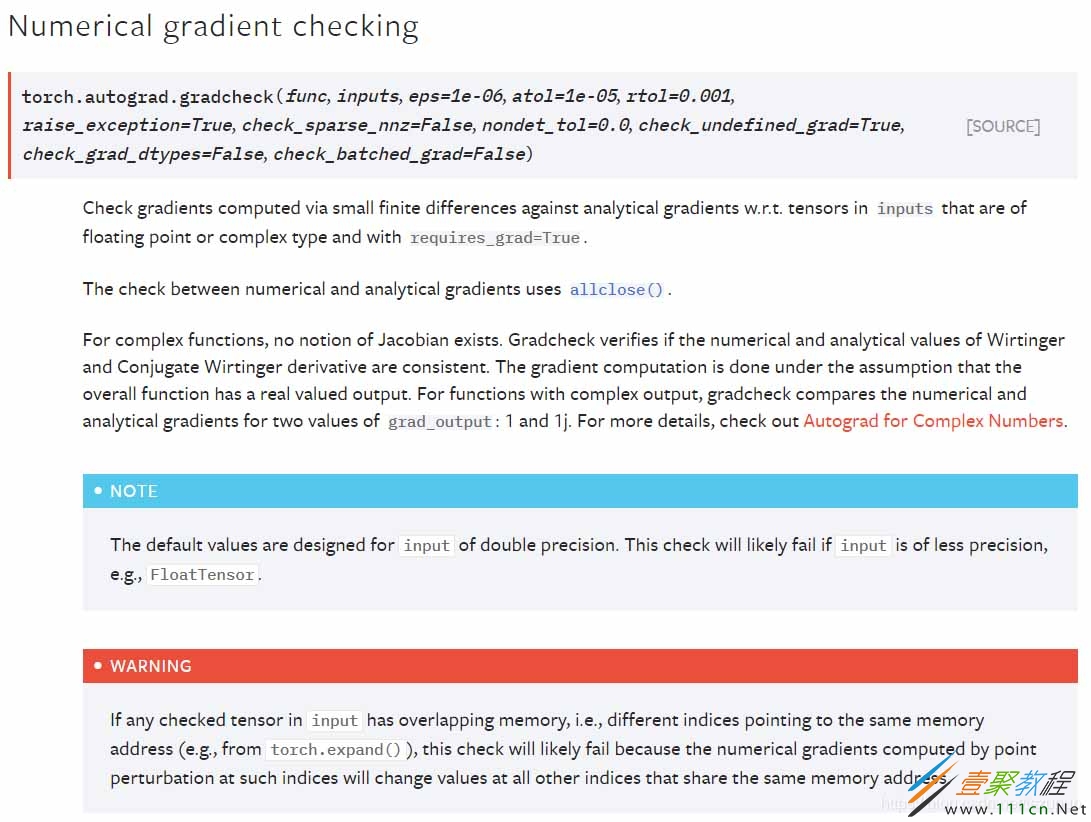
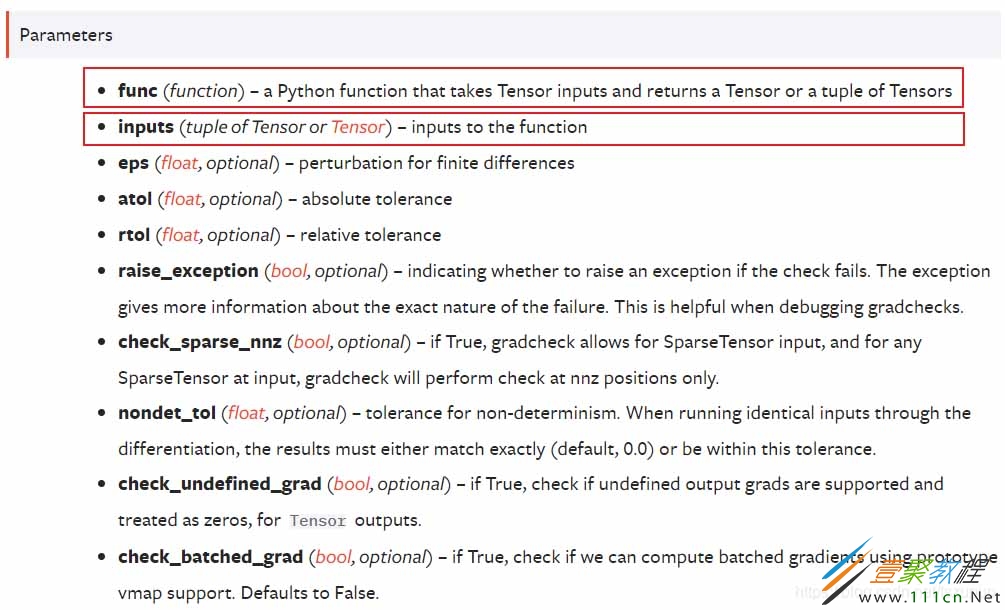
首先看一下官方文档中关于该函数的介绍:
可以看到官方文档中介绍了该函数基于何种方法,以及其参数列表,下面给出几个例子介绍其使用方法,注意:
Tensor需要是双精度浮点型且设置requires_grad = True
第一个例子:检查某一操作是否可导
from torch.autograd import gradcheck
import torch
import torch.nn as nn
inputs = torch.randn((10, 5), requires_grad=True, dtype=torch.double)
linear = nn.Linear(5, 3)
linear = linear.double()
test = gradcheck(lambda x: linear(x), inputs)
print("Are the gradients correct: ", test)
输出为:
Are the gradients correct: True
第二个例子:检查某一网络模型是否可导
from torch.autograd import gradcheck
import torch
import torch.nn as nn
# 定义神经网络模型
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.net = nn.Sequential(
nn.Linear(15, 30),
nn.ReLU(),
nn.Linear(30, 15),
nn.ReLU(),
nn.Linear(15, 1),
nn.Sigmoid()
)
def forward(self, x):
y = self.net(x)
return y
net = Net()
net = net.double()
inputs = torch.randn((10, 15), requires_grad=True, dtype=torch.double)
test = gradcheck(net, inputs)
print("Are the gradients correct: ", test)
输出为:
Are the gradients correct: True
二、Pytorch求导
1.标量对矩阵求导
验证:
>>>import torch
>>>a = torch.tensor([[1],[2],[3.],[4]]) # 4*1列向量
>>>X = torch.tensor([[1,2,3],[5,6,7],[8,9,10],[5,4,3.]],requires_grad=True) #4*3矩阵,注意,值必须要是float类型
>>>b = torch.tensor([[2],[3],[4.]]) #3*1列向量
>>>f = a.view(1,-1).mm(X).mm(b) # f = a^T.dot(X).dot(b)
>>>f.backward()
>>>X.grad #df/dX = a.dot(b^T)
tensor([[ 2., 3., 4.],
[ 4., 6., 8.],
[ 6., 9., 12.],
[ 8., 12., 16.]])
>>>a.grad b.grad # a和b的requires_grad都为默认(默认为False),所以求导时,没有梯度
(None, None)
>>>a.mm(b.view(1,-1)) # a.dot(b^T)
tensor([[ 2., 3., 4.],
[ 4., 6., 8.],
[ 6., 9., 12.],
[ 8., 12., 16.]])
2.矩阵对矩阵求导
验证:
>>>A = torch.tensor([[1,2],[3,4.]]) #2*2矩阵
>>>X = torch.tensor([[1,2,3],[4,5.,6]],requires_grad=True) # 2*3矩阵
>>>F = A.mm(X)
>>>F
tensor([[ 9., 12., 15.],
[19., 26., 33.]], grad_fn=)
>>>F.backgrad(torch.ones_like(F)) # 注意括号里要加上这句
>>>X.grad
tensor([[4., 4., 4.],
[6., 6., 6.]])
注意:
requires_grad为True的数组必须是float类型
进行backgrad的必须是标量,如果是向量,必须在后面括号里加上torch.ones_like(X)
相关文章
- 《弓箭传说2》新手玩法介绍 01-16
- 《地下城与勇士:起源》断桥烟雨多买多送活动内容一览 01-16
- 《差不多高手》醉拳龙技能特点分享 01-16
- 《鬼谷八荒》毕方尾羽解除限制道具推荐 01-16
- 《地下城与勇士:起源》阿拉德首次迎新春活动内容一览 01-16
- 《差不多高手》情圣技能特点分享 01-16