java排序算法之快速排序代码示例

本篇文章小编给大家分享一下java排序算法之快速排序代码示例，文章代码介绍的很详细，小编觉得挺不错的，现在分享给大家供大家参考，有需要的小伙伴们可以来看看。

简单介绍

快速排序（Quicksort）是对冒泡排序的一种改进。

基本思想

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

(1)首先设定一个分界值（基准值），通过该分界值将数组分成左右两部分。

(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

该思想可以概括为：挖坑填数 + 分治法。

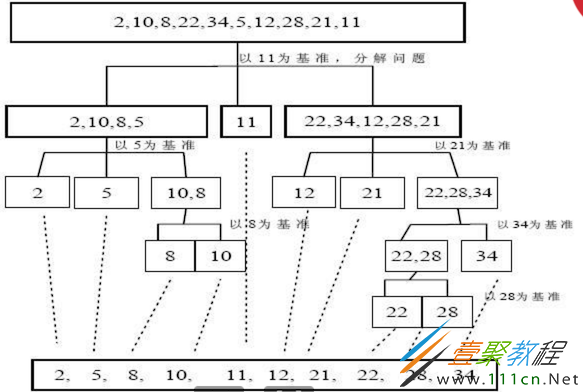
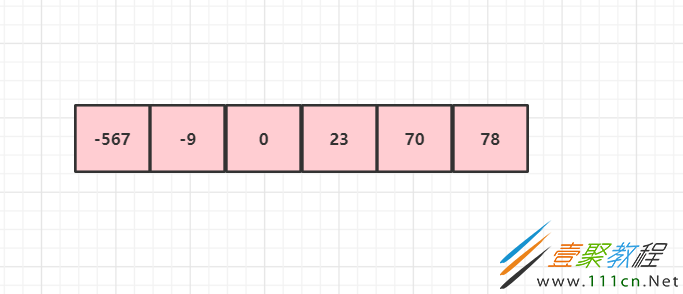
比如如下的示意图：

上图以 最后一个元素的值 作为基准

比基准值小的，排在左侧，比基准值大的排在右侧

然后再以分好的部分重复以上操作，直到每个部分中只有一个数据时，就排好序了

思路分析

基本思想如上，但是实现思路有多种，一般取基准值都是以首尾或者中间，这里使用数组中间的作为基准值，进行讲解。

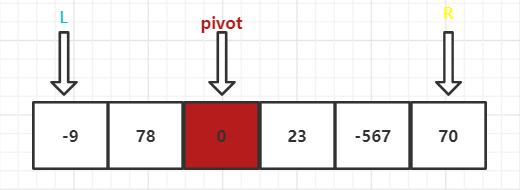
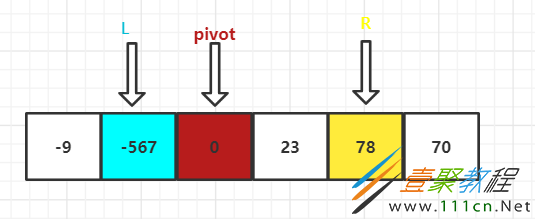
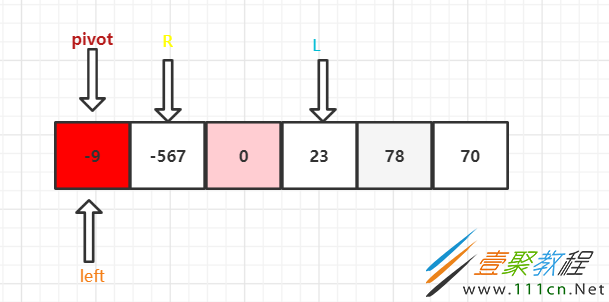
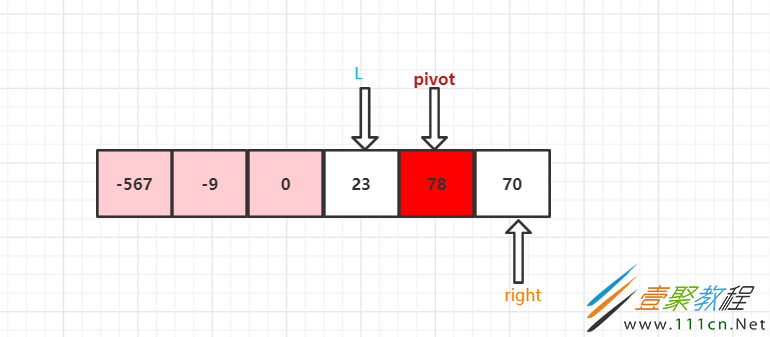
原始数组：arr = [-9,78,0,23,-567-70]

设置两个变量，左下标L = 0，右下标R = 数组大小 - 1，选数组中间的值为基准值，pivot = arr[(L + R )/ 2],基准值为 0。再用两个变量保存 左下标 和 右下标，left = L和right = R，用于后面的排序做准备。

可以看到，pivot把数组分成了两组

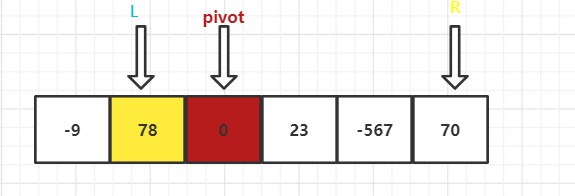
左边一组，从左到右，挨个与 基准值 比较，找出比基准值大的值，跳出查找循环

右边一组，从右到左，挨个与 基准值 比较，找出比基准值小的值，跳出查找循环

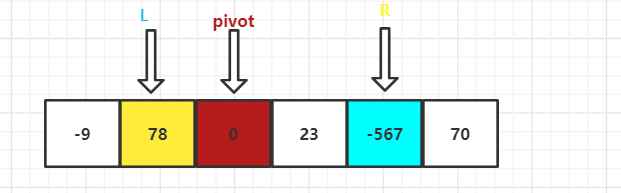
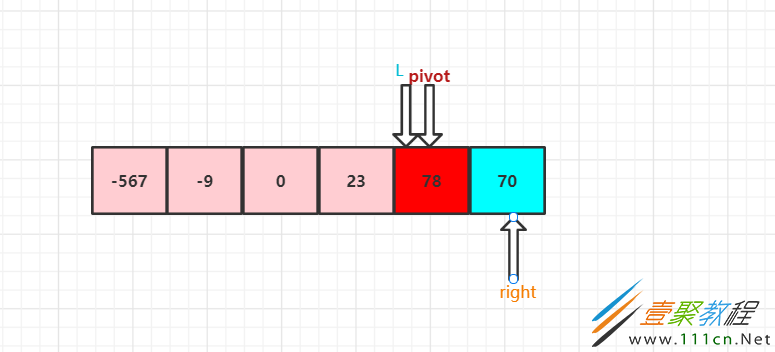
可以看到左右两组各找到一个对应的值，那么就让他们进行交换

然后继续找，直到左右两边碰到，

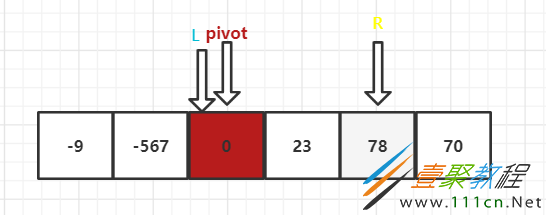
可以看到左边的组已经找完了，L指向了基准值，那就跳出查找循环，右边组开始查找，

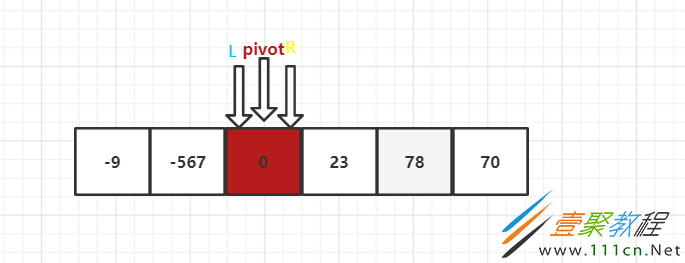
但是我们可以看到右边的数也都符合规则，所以R也循环遍历到了基准值的位置，此时L和R已经碰到一起了，这一轮就结束。这一轮就称为快速排序。

继续对分出来的小组，进行上述的快速排序操作，直到组内只剩下一个数时，则排序完成。

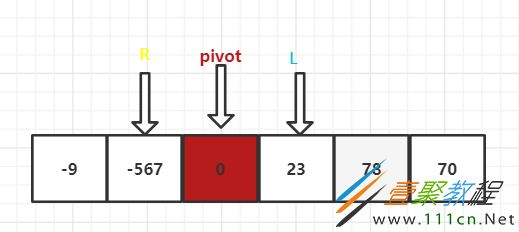
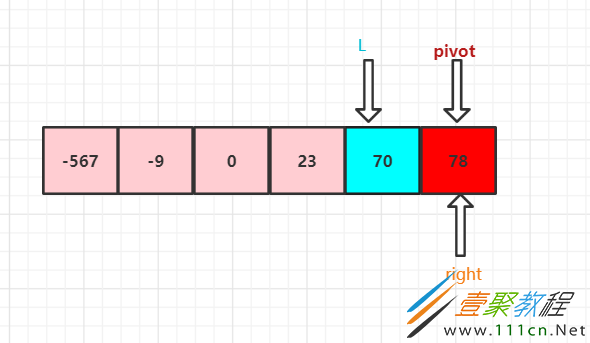
将L和R分别前进一步和后退一步，

如图，就可以再次利用这两个变量，对两组进行快速排序了。

先对左边的组进行快速排序，同样进行上面的操作，

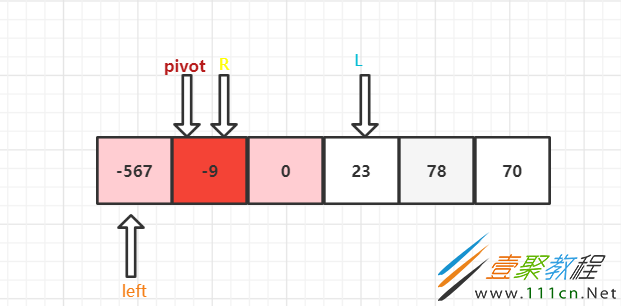
这里就用到了上一次快速循环所保存的left和right（上图没有画出来）了。

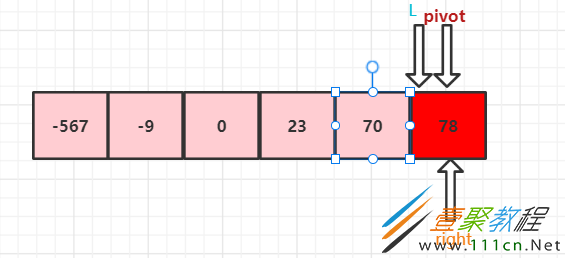
因为这里left直接就指向了pivot，所以不用进行移动查找了。R跟pivot进行比较 ，-567 < -9 ，R和left进行交换，得到如下图，注：pivot是一个值,不是引用类型

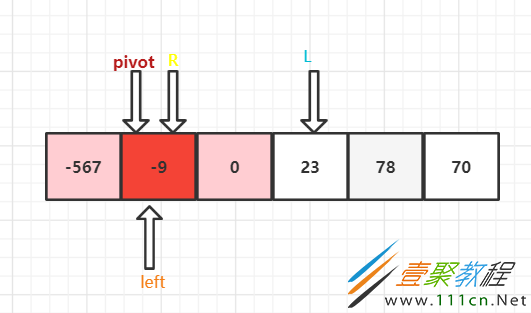
因为R和left没有碰头，所以还得进行一次循环比较。因为R就在基准点这，所以不移动，R和pivot比较，-9 > -567 ， 所以left前进一步，

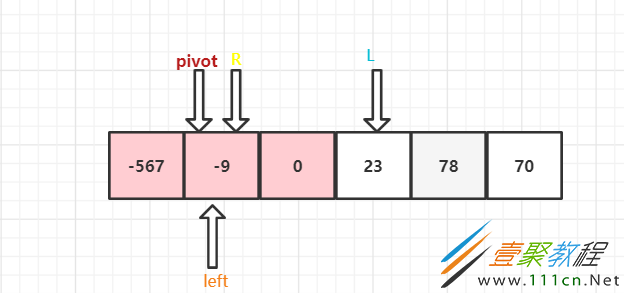
此时R和left已经碰到一起了，这一轮就结束了。

右边的组也是同样的道理，这里就不作过多的解析了

l ------------ pivot --------------- r
一组从左往右找               一组从右往左找

可以看到，分组后，可以使用递归，对这一组继续分组，然后对他们进行快速排序。

代码实现

推导实现

推导法先实现第一轮

    @Test
    public void processDemo() {
        int arr[] = {-9, 78, 0, 23, -567, 70};
        System.out.println("原始数组：" + Arrays.toString(arr));
        processQuickSort(arr, 0, arr.length - 1);
    }

    /**
     * @param arr
     * @param left  左边这一组的下标起始点，到中间值，则为一组
     * @param right 右边这一组的下标结束点，到中间值，则为一组
     */
    public void processQuickSort(int[] arr, int left, int right) {
        /*
         基本思想：选择一个基准值，将基准值小分成一组，比基准值大的分成一组。
         这里的实现思路：
            1. 挑选的基准值为数组中间的值
            2. 中间值就把数组分成了两组
            3. 左边一组，从左到右，挨个与 基准值 比较，找出比基准值大的值
            4. 右边一组，从右到左，挨个与 基准值 比较，找出比基准值小的值
            5. 左右两边各找到一个值，那么就让这两个值进行交换
            6. 然后继续找，直到左右两边碰到，这一轮就结束。这一轮就称为快速排序
            7. 继续对分出来的小组，进行上述的快速排序操作，直到组内只剩下一个数时，则排序完成

            l ------------ pivot --------------- r
            一组从左往右找               一组从右往左找
         */
        int l = left;
        int r = right;
        // 中心点，让这个点作为基准值
        int pivot = arr[(left + right) / 2];
        // 当他们没有碰到的时候，说明还这一轮还可以继续找
        while (l < r) {
            // 左边组：当找到大于基准值时，退出循环，则表示该值需要交换到右侧去: arr[l] > pivot
            //      也就是说，如果 arr[l] < pivot，则表示还没有找到比基准值大的数
            //      注意：不能等于 pivort，因为最差的情况没有找到，则最后 arr[l] 就是 pivot 这个值，也同样退出循环
            while (arr[l] < pivot) {
                l++; // 所以让左边这一组继续找
            }

            // 右边组：当找到小于基准值时，退出循环，则表示该值需要交换到左侧去：arr[r] < pivot
            //      也就是说，如果 arr[l] > pivot，则表示还没有找到比基准值小的数
            //注意：这里也同样跟上面一样，不能等于 pivort
            while (arr[r] > pivot) {
                r--;//让右边组继续找
            }

            // 当左侧与右侧相碰时，说明两边都没有找到，这一轮不用进行交换
            // 等于表示，找到了中间的下标
            if (l >= r) {
                break;
            }

            // 当找到时，则两数进行交换。
            //注意：这里可能会出现有一组已经找完了，或者没有找到，但是另一组找到了，所以一个是指向 pivot 的，
            //另一个则是指向要交换的数,交换后 pivot的值在数组中的位置会发生改变，下次的交换方式就会发生变化。这个地方要动脑筋想想。
            int temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            // 当交换后，
            // 当数组是： {-9, 78, 0, -23, 0, 70}  时（pivot的值在数组中有多个），就可以验证这里的逻辑
            // 如果没有这个判定，将会导致，l 永远 小于 r。循环不能退出来的情况，就出现死循环了
            if (arr[l] == pivot) {
                /*
                  l 自己不能往前移动 一步，因为当交换完成后为：{-9, 0, 0, -23, 78, 70}
                  l = 1,arr[l] = 0
                  r = 4,arr[r] = 78
                  再经过一次循环后
                  l = 1,arr[l] = 0
                  r = 3,arr[r] = -23
                  交换后数组为：{-9，-23，0，0，78，70}
                  此时 l = 1，arr[l] = -23;r = 3,arr[r] = 0
                  又经过一次循环后
                  l = 2,arr[l] = 0
                  r = 3,arr[r] = 0
                  数组为：{-9，-23，0，0，78，70}
                  进入了死循环
                  这里好好动脑子想想
                  
                  这里为什么是用r-=1呢？是因为if里面的条件是arr[l] == pivot，如果要排序的数组中不存在多个和基准值相等的值，
                  那么用l+=1的话，l就会跑过分界线（基准值），跑到另一组去，这个算法也就失败了，
                  还有一个原因是，r 是刚刚交换过的，一定比 基准值大，所以没有必要再和基准值比较了
                 */
                r -= 1;
            }
            // 这里和上面一致，如果说，先走了上面的 r-=1
            // 这里也满足（也就是说有多个值和基准值相等），那么说明，下一次是相同的两个值，一个是 r == 一个是基准值
            // 但是他们是相同的值，r后退一步 l前进一步，不影响。但是再走这完这里逻辑时，就会导致  l > r，退出整个循环
            if (arr[r] == pivot) {
                l += 1;
            }
        }
        System.out.println("第 1 轮排序后：" + Arrays.toString(arr));
    }

注意：上述的算法特别是边界判定，就是上面「当交换后」对r-=1的这个边界判定时，有点难以理解，但是一定要理解为什么要这样写。

测试信息输出

原始数组：[-9, 78, 0, 23, -567, 70]

第 1 轮排序后：[-9, -567, 0, 23, 78, 70]

那么如何向左递归和右递归呢？在上面的代码后面接着实现如下

        System.out.println("第 1 轮排序后：" + Arrays.toString(arr));

		/*
		if (l >= r) {
                break;
            }
            循环从这条代码中跳出就会l = r
		*/
        // 如果 l = r，会出现死循环，出现栈溢出
		//这里也要动脑子想想
        if (l == r) {
            l++;
            r--;
        }

        // 开始左递归
        // 上面算法是 r--，l++ ，往两组的中间走，当 left < r 时，表示还可以继续分组
        if (left < r) {
            processQuickSort(arr, left, r);
        }

        if (right > l) {
            processQuickSort(arr, l, right);
        }

完整实现

完整实现和推导实现其实差不多了，为了加深记忆，自己按照基本思想和思路分析，默写。

  /**
     * 快速排序默写实现
     * 
     *     基本思想：通过一趟将要排序的数据，分隔成独立的两个部分，一部分的所有数据都比另一部分的所有数据要小。
     *     思路分析：
     *      {-9, 78, 0, 23, -567, 70};  length=6
     *      1. 挑选中间的值作为 基准值：(0 + (6 -1))/2= [2] = 0
     *      2. 左侧 left 部分，从 0 开始到中间值 -1： 0,1: -9, 78,找出一个比基准值大的数
     *      3. 右侧 right 部分，从中间值 + 1 到数组大小-1：3,5：23,-567, 70，找出一个比基准值小的数
     *      4. 如果找到，则将他们进行交换，这样一轮下来，就完成了一次快速排序：一部分的所有数据都比另一部分的所有数据要小。
     *      4. 如果左侧部分还可以分组，则进行左侧递归调用
     *      5. 如果右侧部分还可以分组，则进行右侧递归调用
     *
     *    简单说：一轮快速排序示意图如下：
     *                   中间的基准值
     *      l ------------ pivot --------------- r
     *      一组从左往右找               一组从右往左找
     *      找到比基准值大的数          找出一个比基准值小的数
     *                    然后进行交换
     * 
     */
    @Test
    public void quickSortTest() {
        int arr[] = {-9, 78, 0, 23, -567, 70};
//        int arr[] = {-9, 78, 0, -23, 0, 70}; // 在推导过程中，将会导致交换异常的数组，在这里不会出现那种情况
        int left = 0;
        int right = arr.length - 1;
        System.out.println("原始数组：" + Arrays.toString(arr));
        quickSort(arr, left, right);
        System.out.println("排序后：" + Arrays.toString(arr));
    }

    public void quickSort(int[] arr, int left, int right) {
        // 找到中间值
        int pivotIndex = (left + right) / 2;
        int pivot = arr[pivotIndex];
        int l = left;
        int r = right;
        while (l < r) {
            // 从左往右找，直到找到一个数，比基准值大的数
            while (arr[l] < pivot) {
                l++;
            }
            // 从右往左找，知道找到一个数，比基准值小的数
            while (arr[r] > pivot) {
                r--;
            }
            // 表示未找到
            if (l >= r) {
                break;
            }
            // 进行交换
            int temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            // 那么下一轮，左侧的这个值将不再参与排序，因为刚交换过，一定比基准值小
            // 那么下一轮，右侧的这个值将不再参与排序，因为刚交换过，一定比基准值大
            r--;
            l++;
        }

        // 当一轮找完后，没有找到，则是中间值时，
        // 需要让他们擦肩而过，也就是重新分组，中间值不再参与分组
        // 否则，在某些情况下，会进入死循环
        if (l == r) {
            l++;
            r--;
        }
        // 如果左侧还可以继续分组，则继续快排
        // 由于擦肩而过了，那么左侧的组值，则是最初的开始与中间值的前一个，也就是这里得到的 r
        if (left < r) {
            quickSort(arr, left, r);
        }
        if (right > l) {
            quickSort(arr, l, right);
        }
    }

另外，在实现的过程中，将某些代码为什么要那样判断边界，进行了梳理。你会发现上述代码和推导的代码有一个地方不一样。这个是我自己按逻辑进行的改进，更容易看明白一些。目前未发现 bug，如果有错请评论指出，毕竟这个算法还是有点难的。

大数据量耗时测试

    /**
     * 大量数据排序时间测试
     */
    @Test
    public void bulkDataSort() {
        int max = 80000;
//        int max = 8;
        int[] arr = new int[max];
        for (int i = 0; i < max; i++) {
            arr[i] = (int) (Math.random() * 80000);
        }
        if (arr.length < 10) {
            System.out.println("原始数组：" + Arrays.toString(arr));
        }
        Instant startTime = Instant.now();
//        processQuickSort(arr, 0, arr.length - 1);  // 和老师的原版代码对比，结果是一样的
        quickSort(arr, 0, arr.length - 1);
        if (arr.length < 10) {
            System.out.println("排序后：" + Arrays.toString(arr));
        }
        Instant endTime = Instant.now();
        System.out.println("共耗时：" + Duration.between(startTime, endTime).toMillis() + " 毫秒");
    }

多次运行输出

共耗时：40 毫秒

共耗时：52 毫秒

共耗时：36 毫秒

共耗时：31 毫秒

性能分析

快速排序的一次划分算法从两头交替搜索，直到low和hight重合，因此其时间复杂度是O(n)；而整个快速排序算法的时间复杂度与划分的趟数有关。

理想的情况是，每次划分所选择的中间数恰好将当前序列几乎等分，经过log2n趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为O(nlog2n)。

最坏的情况是，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为O(n2)。

为改善最坏情况下的时间性能，可采用其他方法选取中间数。通常采用“三者值取中”方法，即比较H->r[low].key、H->r[high].key与H->r[(low+high)/2].key，取三者中关键字为中值的元素为中间数。

可以证明，快速排序的平均时间复杂度也是O(nlog2n)。因此，该排序方法被认为是目前最好的一种内部排序方法。

从空间性能上看，尽管快速排序只需要一个元素的辅助空间，但快速排序需要一个栈空间来实现递归。最好的情况下，即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表，所需栈的最大深度为log2(n+1)；但最坏的情况下，栈的最大深度为n。这样，快速排序的空间复杂度为O(log2n)。