最新下载
热门教程
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
java编程约瑟夫问题实例分析
时间:2022-06-29 02:33:20 编辑:袖梨 来源:一聚教程网
一、简介
约瑟夫问题(有时也称为约瑟夫斯置换,是一个出现在计算机科学和数学中的问题。在计算机编程的算法中,类似问题又称为约瑟夫环。又称“丢手绢问题”.)
例子:
len个人围成一个圈,玩丢手绢游戏。从第k个人开始,从1开始数数,当数到m时,数m的人就退出圈子,当圈子只剩下一个人为止。
问题分析与算法设计
约瑟夫问题并不难,但求解的方法很多;题目的变化形式也很多。这里给出一种实现方法。
题目中len个人围成一圈,因而启发我们用一个循环的链来表示,可以使用结构数组来构成一个循环链。结构中有两个成员,其一为指向第一个孩子的头节点,另一个为作为判断的节点temp(负责跑龙套)。
具体代码如下:
package demo11;
/**
* 约瑟夫问题, 化为丢手绢
*
* @author tianq 思路:建立一个Child类 一个循环列表类CyclLink
*/
public class demo11 {
public static void main(String[] args) {
CyclLink cyclink = new CyclLink();
cyclink.setLen(15);
cyclink.createLink();
cyclink.setK(2);
cyclink.setM(2);
cyclink.show();
cyclink.play();
}
}
// 先建立一个孩子类
class Child {
// 孩子的标识
int no;
Child nextChild;
// 指向下一个孩子
public Child(int no) {
// 构造函数给孩子一个id
this.no = no;
}
}
class CyclLink {
// 先定义一个指向链表第一个小孩的引用
// 指向第一个小孩的引用,不能动
Child firstChild = null;
Child temp = null;
int len = 0;
// 表示共有几个小孩
int k = 0;
//开始的孩子
int m = 0;
//数到几推出
// 设置m
public void setM(int m) {
this.m = m;
}
// 设置链表的大小
public void setLen(int len)
{
this.len = len;
}
// 设置从第几个人开始数数
public void setK(int k) {
this.k = k;
}
// 开始play
public void play() {
Child temp = this.firstChild;
// 1.先找到开始数数的人
for (int i = 1; i < k; i++) {
temp = temp.nextChild;
}
while (this.len != 1) {
// 2.数m下
for (int j = 1; j < m; j++) {
temp = temp.nextChild;
}
// 找到要出圈的前一个小孩
Child temp2 = temp;
while (temp2.nextChild != temp) {
temp2 = temp2.nextChild;
}
// 3.将数到m的小孩,退出
temp2.nextChild = temp.nextChild;
// 让temp指向下一个数数的小孩
temp = temp.nextChild;
// this.show();
this.len--;
}
// 最后一个小孩
System.out.println("最后出圈" + temp.no);
}
// 初始化环形链表
public void createLink() {
for (int i = 1; i <= len; i++) {
if (i == 1) {
// 创建第一个小孩
Child ch = new Child(i);
this.firstChild = ch;
this.temp = ch;
} else {
if (i == len) {
// 创建第一个小孩
Child ch = new Child(i);
temp.nextChild = ch;
temp = ch;
temp.nextChild = this.firstChild;
} else {
// 继续创建小孩
Child ch = new Child(i);
temp.nextChild = ch;
temp = ch;
}
}
}
}
// 打印该环形链表
public void show() {
Child temp = this.firstChild;
do {
System.out.print(temp.no + " ");
temp = temp.nextChild;
}
while (temp != this.firstChild);
}
}
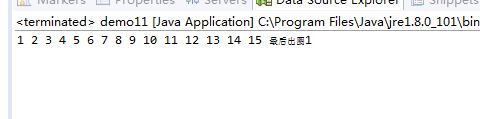
结果:
相关文章
- 《弓箭传说2》新手玩法介绍 01-16
- 《地下城与勇士:起源》断桥烟雨多买多送活动内容一览 01-16
- 《差不多高手》醉拳龙技能特点分享 01-16
- 《鬼谷八荒》毕方尾羽解除限制道具推荐 01-16
- 《地下城与勇士:起源》阿拉德首次迎新春活动内容一览 01-16
- 《差不多高手》情圣技能特点分享 01-16